Можно ли в сечении цилиндра плоскостью получить прямоугольник

Геометрия. 11 класс

Геометрия, 11 класса

Урок №6. Тела вращения. Цилиндр

Перечень вопросов, рассматриваемых в теме:

• тело вращения;
• цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения;
• площади поверхностей цилиндра.

Глоссарий по теме

Цилиндрическая поверхность — это поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность.

Эти прямые — образующие цилиндрической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости — ось цилиндрической поверхности.

Цилиндр — тело, ограниченное цилиндрической поверхностью и двумя кругами.

Круги — основания цилиндра; отрезки образующих, заключённые между основаниями — образующие цилиндра; образованная ими часть цилиндрической поверхности — боковая поверхность.

Ось цилиндрической поверхности называется осью цилиндра.

Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.

Сечение — изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение — вариант сечения, при котором плоскость проходит через ось тела.

Развёртка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а другая длине окружности основания.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10-11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни — М. : Просвещение, 2014. — 255, сс.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10-11 кл. : учеб. для общеобразоват. учреждений — М.: Дрофа, 2009. — 235, : ил., ISBN 978-5-358-05346-5, сс. 77-79.

Открытые электронные ресурсы:

Образовательный портал «Решу ЕГЭ». https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные определения

Определение

Цилиндрической поверхностью называется поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность (см.рис.).

Определение

Сами прямые называют образующими цилиндрической поверхности.

Определение

Прямая, проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.

Так как все образующие и ось перпендикулярны плоскости ????, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).

Если построить ещё одну плоскость ????, которая будет параллельна плоскости ????, то отрезки образующих, заключённые между плоскостями ???? и ???? будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости ????, дают окружность, равную окружности, лежащей в плоскости ????.

Определение

Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях ???? и ????) называется цилиндром.

Определение

Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности — боковой поверхностью цилиндра.

Определение

Ось цилиндрической поверхности называется осью цилиндра.

Определение

Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания — радиусом цилиндра.

Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.

2. Сечения цилиндра различными плоскостями

Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого — образующие, а две другие — диаметры оснований цилиндра.

Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.

Если секущая плоскость проходит параллельно оси цилиндра, но не содержит саму ось, то сечение является прямоугольником две стороны которого — образующие, а две другие — отрезки, соединяющие эти образующие в верхнем и в нижнем основании (ЗАМЕЧАНИЕ: эти отрезки меньше диаметров оснований цилиндра).

3. Основные формулы

Формула для вычисления площади боковой поверхности цилиндра: Sбок=2????RL.

То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2????R(R+L).

Примеры и разбор решения заданий тренировочного модуля

1. Дан цилиндр.

Выберите значение площади его боковой поверхности

1) 60π

2) 192π

3) 120π

4) 36π

Решение:

Площадь боковой поверхности вычисляется по формуле: S=2πRL.

R=6, L=10

Подставим: S=2π·6·10=120π.

Ответ: 3) 120π

2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу 1200. Образующая цилиндра равна 6, расстояние от оси до секущей плоскости равно 1. Найдите площадь сечения.

Решение:

Сделаем чертеж:

По условию задачи ∟АОВ=1200, ВС= 6.

Расстояние от оси до секущей плоскости — отрезок ОН=1.

Найдем сторону АВ сечения.

∆ОНВ — прямоугольный.

В ∆ОНВ: ОН=1, ∟НОВ=600.

НВ=ОН·tg600=1·.

Sсеч=6·=18

Ответ: 18

3. Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.

Решение:

Sполн =2πR(R+L)

По условию задачи L=R+6.

144π=2πR(R+R+6).

Получили квадратное уравнение относительно радиуса:

R2+6R-72=0

R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.

Ответ: 12.

Источник

Цилиндры

Основные определения и свойства цилиндра

Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).

Рис.1

Если из каждой точки окружности опустить перпендикуляр на плоскость β, то основания этих перпендикуляров образуют на плоскости β окружность радиуса r, центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Рис.2

Определение 1.

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра. Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра.

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.

Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

Рис.3

На рисунке 3 изображено одно из осевых сечений цилиндра — прямоугольник AA1B1B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Рис.4

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Объем цилиндра. Площадь боковой поверхности цилиндра.

Площадь полной поверхности цилиндра

Для цилиндра с радиусом r и высотой h (рис. 5)

Рис.5

введем следующие обозначения

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

Sосн = πr2,

V = Sоснh = πr2h,

Sбок= 2πrh,

Sполн = 2πr2 + 2πrh =

= 2π(r + h).

Замечание 7. Формула объема цилиндра V = πr2h может быть получена из формулы объема правильной n — угольной призмыформулы объема правильной n — угольной призмы

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Источник

Тест с ответами: “Цилиндр”

1. Дан цилиндр, длина диаметра основания которого в два раза меньше длины образующей. Объем этого цилиндра равен 108п. Вычислите диаметр основания:

а) 6 +

б) 14

в) 12

2. Что представляет сечение цилиндра, проведенное плоскостью, перпендикулярно оси:

а) овал

б) круг +

в) прямоугольник

3. Вычислите длину радиуса основания равностороннего цилиндра, площадь полной поверхности которого равна 24п:

а) 48

б) 12

в) 2 +

4. Что представляет осевое сечение цилиндра:

а) прямоугольник +

б) треугольник

в) овал

5. Объем цилиндра равен произведению площади … на высоту:

а) стороны

б) вершины

в) основания +

6. Что представляет боковая поверхность цилиндра:

а) треугольник

б) прямоугольник +

в) круг

7. Сечение, проходящее параллельно основаниям цилиндра, является:

а) прямоугольником

б) квадратом

в) кругом +

8. Объем цилиндра равен 64π, а площадь боковой поверхности — 32π. Найдите площадь полной поверхности цилиндра, деленную на π:

а) 64 +

б) 72

в) 48

9. Цилиндр, осевым сечением которого является квадрат, называется:

а) правильным круглым

б) эллиптическим

в) равносторонним +

10. Про прямые круговые цилиндры C1 и C2 известно, что у C1 радиус основания в два раза больше, чем у C2, но у C2 высота в три раза больше, чем у C1. Найдите отношение объёма цилиндра C2 к объёму C1:

а) 1

б) 0,75 +

в) 1,2

11. Если диаметр основания и образующая цилиндра равны друг другу, то осевым сечением является:

а) квадрат +

б) круг

в) прямоугольник

12. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали:

а) 24 л

б) 14 л +

в) 12 л

13. Геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её:

а) цилиндр +

б) конус

в) квадрат

14. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра:

а) 1,20

б) 1,5

в) 1,25 +

15. Сечение, проходящее параллельно оси цилиндра, может быть:

а) либо прямоугольником, либо квадратом +

б) только квадратом

в) только прямоугольником

16. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого:

а) 18 см

б) 3 см +

в) 9 см

17. Если диаметр основания и образующая цилиндра не равны друг другу, то осевым сечением является:

а) квадрат

б) круг

в) прямоугольник +

18. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали:

а) 1100 см3

б) 1000 см3 +

в) 100 см3

19. Вычислите длину высоты равностороннего цилиндра, площадь осевого сечения которого равна 25:

а) 50

б) 12,5

в) 5 +

20. Пусть V, r, h соответственно объем, радиус и высота цилиндра. Найдите объем, если r=2√2 cм, h=3 см:

а) 43π см3

б) 24π см3 +

в) 31π см3

21. Сколько образующих можно провести в цилиндре:

а) много +

б) одну

в) две

22. Радиус основания цилиндра равен 7, а высота — 10. Найдите площадь боковой поверхности цилиндра, деленную на π:

а) 124

б) 140 +

в) 104

23. Какой вид не может иметь сечение цилиндра:

а) овал

б) квадрат

в) треугольник +

24. Шар вписан в цилиндр. Площадь поверхности шара равна 41. Найдите площадь полной поверхности цилиндра:

а) 60

б) 61,5 +

в) 55

25. Вращением какой геометрической фигуры можно получить цилиндр:

а) прямоугольного треугольника вокруг гипотенузы

б) прямоугольного треугольника вокруг катета

в) прямоугольника вокруг одной из сторон +

26. Площадь боковой поверхности цилиндра равна 18π, а диаметр основания равен 9. Найдите высоту цилиндра:

а) 4

б) 2 +

в) 36

27. Площадь полной поверхности цилиндра:

а) S=2п(r+h) +

б) S= r(r+h)

в) S=пr(r+h)

28. Поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей):

а) поверхность основания цилиндра

б) коническая поверхность

в) цилиндрическая поверхность +

29. Площадь боковой поверхности цилиндра:

а) S=пrh +

б) S=2r

в) S=r2

30. Отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка:

а) сторона цилиндра

б) высота цилиндра +

в) вершина цилиндра

Источник

Сечение цилиндра: определение, виды, его образующая

Кратко о цилиндре

Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.

Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.

Осевое сечение

Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти площадь сечения

Формула 1

(S = d*h,)

где (d) — диаметр, а (h) — высота всей фигуры.

Источник: reader.lecta.rosuchebnik.ru

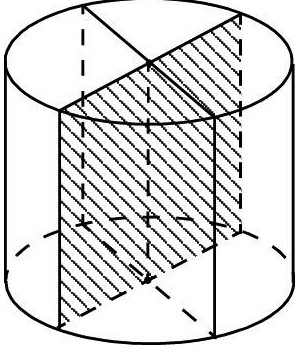
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).

Формула 2

(S = a*h, )

где (a) — хорда.

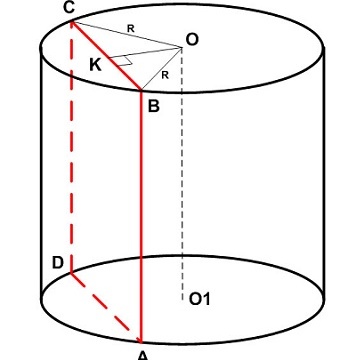
Источник: bezikev.ru

Осевое сечение наклонного цилиндра

Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.

Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:

(S = d * b * sin(α))

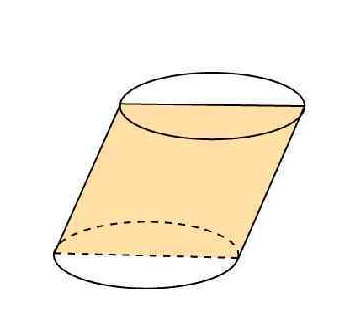
Источник: present5.com

Примеры задач

Рассмотрим пару задач на осевое сечение с решениями.

Задача 1

Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?

Решение

Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:

(Sц = 2pi * r * (r + h))

Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:

(Sц = 2pi * r * (r + 2r) = 6 * pi * r²)

Исходя из этого, будем выражать радиус:

(r = √(Sц / (6*pi)))

Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:

(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi))

Подставим известные данные ((Sц = 100см^2)) и получим площадь сечения (S = 21,23 см²).

Ответ: (S = 21,23 см²).

Задача 2

Дано: ABCD — осевое сечение цилиндра. Площадь сечения (Sc) равна (10 м²), а площадь основания (Sо- 5 м²). Найти высоту цилиндра.

Решение

Так как площадь основания — круг, то (Sо = pi * r²). Тогда (r = √(Sо/pi) = √(5/pi).)

Так как площадь сечения — прямоугольник, то (Sc = AB * BC = h * 2r.) Тогда (h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).)

Ответ: (h = √(5pi).)

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Источник