Можно ли с помощью простого механизма получить выигрыш в работе
Содержание статьи
Простые механизмы.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм — это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы — это рычаг и наклонная плоскость.
Рычаг.
Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы и . Плечи этих сил равны соответственно и .
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
Неподвижный блок.
Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом . Напомним, что вес тела — это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес прило жен к точке , в которой груз крепится к нити.
К левому концу нити в точке приложена сила .
Плечо силы равно , где — радиус блока. Плечо веса равно . Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство , а во-вторых, в процессе движении груза и нити перемещение точки равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити .
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы «перекатывается» через точку ). Говорят ещё, что через точку проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке крепления груза к нити. Плечо силы равно .
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно . Соответственно, условием равновесия груза является равенство (что мы и видим на рис. 3: вектор в два раза короче вектора ).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) — не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость — это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: «наклонная плоскость с углом «.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом . Эта сила , разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что , поскольку . Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол .
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу . Но для поднятия груза на высоту большее плечо придётся опустить на , и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту над начальным положением, нам нужно пройти путь вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен .
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы из точки в точку на высоту (рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения .
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Источник
62. .
Глава 4. Работа и мощность. Энергия Рассмотренные нами простые механизмы применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу. Естественно, возникает вопрос: позволяя получить выигрыш в силе или в пути, нельзя ли с помощью простых механизмов получить выигрыш и в работе? Для ответа на поставленный вопрос проделаем опыт.
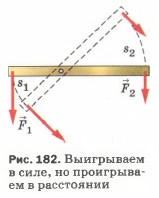
Уравновесив на рычаге две какие-нибудь разные по модулю силы F1 и F2 (рис. 182), приводят рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F2 проходит больший путь s2, а точка приложения большей силы F1 — меньший путь s1. Измерив эти пути и модули сил, находят, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам: Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути. Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу: F1S1 = F2s2, т. e. A1 = A2. Итак, при использовании рычага выигрыша в работе не получают. Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Если мы силу приложим к длинному плечу, то выиграем в силе, но во столько же раз проиграем в расстоянии. Действуя же силой на короткое плечо рычага, мы выиграем в расстоянии, но во столько же раз проиграем в силе.
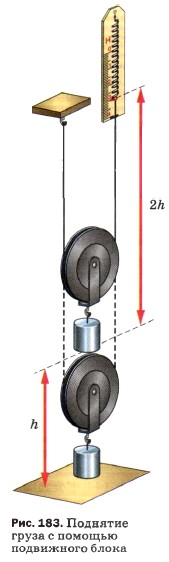
Существует легенда, что Архимед, восхищённый открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я подниму Землю!» Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали точку опоры (которая должна была бы находиться вне Земли) и рычаг нужной длины. Для подъёма Земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например со скоростью 1 м/с , потребовались бы миллионы лет. Не даёт выигрыша в работе и неподвижный блок, в чём легко убедиться на опыте (см. рис. 168). Пути, проходимые точками приложения сил F1 и F2, одинаковы, одинаковы и силы, а значит, одинаковы и работы. Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец верёвки, к которому прикреплён динамометр, как показывает опыт (рис. 183), переместить на высоту 2h. Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок не даёт выигрыша в работе. Многовековая практика показала, что ни один из механизмов не даёт выигрыша в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути. Уже древним учёным было известно правило, применимое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики. Вопросы1. Какое соотношение существует между силами, действующими на рычаг, и плечами этих сил (см. рис. 167)? 2. Какое соотношение существует между путями, пройденными точками приложения сил на рычаге, и этими силами? 3. В чём проигрывают, пользуясь рычагом, дающим выигрыш в силе? 4. Во сколько раз проигрывают в пути, используя для поднятия грузов подвижный блок? 5. В чём состоит «золотое правило» механики? Упражнение 331. С помощью подвижного блока груз подняли на высоту 1,5 м. На какую длину при этом был вытянут свободный конец верёвки? 2. Рабочий с помощью подвижного блока поднял груз на высоту 7 м, прилагая к свободному концу верёвки силу 160 Н. Какую работу он совершил? (Вес блока и силу трения не учитывать.) 3. Как применить блок для выигрыша в расстоянии? 4. Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза; в 6 раз? 5. Решите задачу 2, учитывая вес блока, равный 20 Н. Задание
|
Источник
Тест по физике: Равенство работ при использовании простых механизмов. «Золотое правило» механики (Перышкин 7 класс)
- Главная
- Игры
- Викторины
- Учебные викторины
- Викторины для школы
- Викторины для школы по классам
- Викторины для средней школы
- Викторины по физике
- Викторины по физике для 7 класса
- Викторины по учебнику Перышкина A. В. «Физика. 7 класс»
Выбрав правильный на ваш взгляд вариант ответа, жмите на кнопку «Проверить». Если хотите сразу увидеть правильные ответы, ищите под вопросами ссылку «Посмотреть правильные ответы»
1.
Можно ли с помощью простых механизмов получить выигрыш в работе?
Нельзя
Можно
Можно только с помощью сложных механизмов
2.
Выберете верное утверждение.
Пути, пройденные точками приложения сил на рычаге обратно пропорциональны силам.
Пути, пройденные точками приложения сил на рычаге прямо пропорциональны силам.
Пути, пройденные точками приложения сил на рычаге не зависят от сил, приложенных к телам.
3.
Что такое работа?
Произведение силы на путь.
Произведение пути на скорость.
Произведение ускорения на массу.
4.
В чем измеряется работа?
В Ньютонах
В Ваттах
В Джоулях
5.
Если перемещение тела под действием приложенной силы равно нулю, то чему будет равна работа?
Работа равна нулю
Работа равна силе
Работу невозможно определить
6.
Выберите верное утверждение.
При использовании рычага выигрыша в работе не получают
При использовании рычага выигрыша в энергии не получают
При использовании рычага выигрыша в силе не получают
7.
Выберите правильное утверждение.
Действуя силой, на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проиграем в силе.
Действуя силой, на короткое плечо рычага, мы выигрываем в силе, но во столько же раз проиграем в расстоянии.
Действуя силой, на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проиграем в работе.
8.
Кто автор высказывания: «Дайте мне точку опоры и я переверну землю»?
Архимед
Аристотель
Платон
9.
Дает ли выигрыш в работе неподвижный блок?
Не дает
Дает
Дает частично
10.
Какое утверждение является золотым правилом механики?
Во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии
Во сколько раз выигрываем в силе, во столько раз выигрываем в расстоянии
Во сколько раз проигрываем в силе, во столько раз проигрываем в расстоянии
Источник