Можно ли при умножении чисел получить нуль
Содержание статьи
Умножение на ноль — правило в математике и примеры
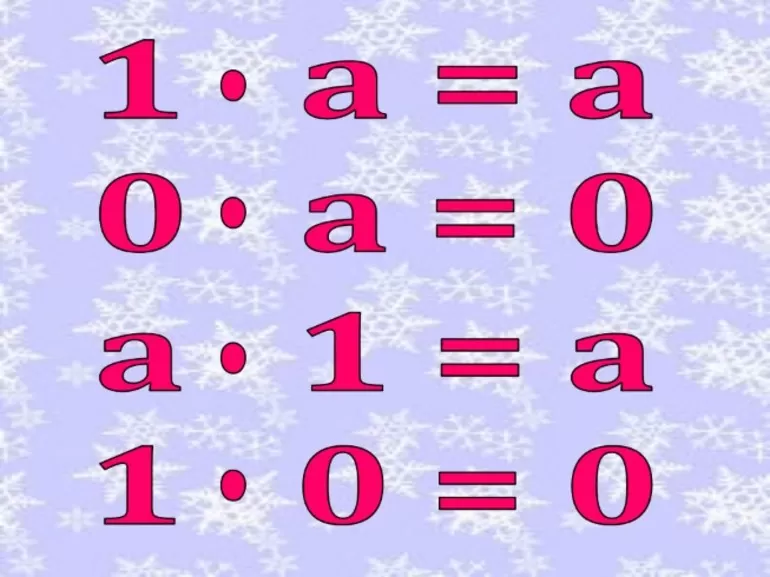
История возникновения
Ноль означает ничто, пустоту. Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.
Но повсеместно применять в вычислениях его начали лишь спустя несколько тысячелетий. Это произошло в Индии. Нулю там придавали не только математический, но и философский смысл. Он означает отсутствие всего, а его форма соответствовала кругу жизни.
Индусы использовали 0 как любое другое число. Его складывали, вычитали, на него умножали. С делением на 0 возникла проблема, но благодаря ей в дальнейшем возникла другая область математики — математический анализ. Идею использования нуля подхватили исламские ученые на Ближнем Востоке и внесли его в арабскую систему счисления.
В Европе до Крестовых походов применялась Римская система счисления. Это непозиционная система, и ноль в ней отсутствует. Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.
Во времена первых Крестовых походов арабские цифры вместе с нолем и позиционной системой счисления пришли в Европу. К этим новшествам сначала отнеслись с большим недоверием. Во Флоренции даже был издан закон о запрещении использования арабских цифр вместе с нулем.
Считалось, что они поощряют мошенничество: 0 легко переделать на цифру 9 или приписать в конце счета, чтобы величина долга возросла многократно. Лишь в XV веке, когда началось развитие в сфере математики и механики, люди оценили преимущество нуля и арабских цифр и стали использовать их повсеместно.
Сложение, умножение, степень
В математике используется несколько действий. Они следующие:
- сложение;
- вычитание;
- умножение;
- деление;
- возведение в степень.
Сложение с нулем обычно вопросов не вызывает. Если к любому числу добавить 0, это значит, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй. То же самое будет, если отнять ноль.
Операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на ноль получается ноль. Это объясняется особенностями операции умножения. Изначально ее определяли как число, прибавленное к самому себе определенное количество раз, что справедливо для натуральных чисел. Так, 5 х 3 = 15. Этот пример можно заменить следующим выражением: 5 + 5 + 5 = 15. То есть число 5 было взято 3 раза. Согласно этому правилу, умножение на 0 числа 5 дает нулевой результат, и 5 х 0 = 0.
Чтобы было нагляднее, можно привести следующий пример:
- если мальчик съел 2 раза по 2 яблока, то окажется, что он позавтракал 4 яблоками;
- если он съел 3 раза по 2 яблока, то в результате получится 6 яблок;
- если же он съел 0 раз по 2 яблока, то ответ будет 0.
Иногда юные скептики выдвигают следующее возражение: допустим, у мальчика в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся в него в руке. Почему же тогда результат равен нулю? Действительно, яблоки из руки никуда не денутся. Но в примере учитываются лишь те из них, которые были съедены, проще говоря, оказались в желудке у мальчика. В последнем случае они туда не попали.
Правило умножения на ноль в математике действительно для любых чисел:
- положительных;
- отрицательных;
- целых;
- дробей;
- разрядных;
- рациональных;
- иррациональных;
- 0 можно умножать на 0.
В любом случае произведение будет нулевым. С нулем можно производить следующие действия:
- Если его разделить на любое ненулевое число, то в результате получится ноль. Правило действительно для положительных и отрицательных чисел.
- Любое число, не равное нулю, можно возвести в нулевую степень, в результате получится 1. Ноль в нулевую степень возводить нельзя, это бессмысленно.
- Нуль можно возвести в любую ненулевую степень, получится нуль. Пример: 02 = 0. Это выражение можно заменить следующим: 0 х 0 =0. Результат будет нулевым согласно правилам умножения.
- Корень из нуля равен нулю.
Деление на ноль
Математики говорят, что четыре арифметических действия: сложение, вычитание, умножение и деление неравноправны. Базовыми считаются первое и третье из них (сложение и умножение), а деление и вычитание — производными.
Например, разность между 5 и 2 равна 3. Это действие также можно записать в виде следующего выражения: Х + 2 = 5. Решением уравнения будет число 3. Аналогичное правило действует и для умножения. Деление 6 на 3 можно записать так: Х * 2 = 3.
Для действий с нулем можно использовать следующий прием. Выражение записывают так: Х * 0 = 0. Здесь X может быть равен любому числу. Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.
Если попытаться найти результат от деления ненулевого числа (например, 5) на ноль, то это действие можно записать так: Х * 0 = 5. Так, при умножении любого числа на ноль получается ноль, у этого уравнения в арифметике нет решения.
Раскрытие неопределенностей
Действиями, связанными с делением на 0, занимается один из разделов высшей математики — математический анализ. В нем используется такое понятие, как бесконечность (бесконечно большая величина). Одно из ее определений — это предел, к которому стремится выражение а/Х при Х, стремящемся к нулю. Здесь а — любое ненулевое действительное число. Если в этом выражении уменьшать значение X, то результат будет увеличиваться, пока, в конце концов, не подойдет к бесконечности. С этой величиной можно делать различные математические действия:
- прибавлять любые числа;
- вычитать числа, не равные бесконечности;
- умножать на значения, не равные 0 и бесконечности;
- возводить в степень, не равную 0.
В результате получится бесконечность. Следующие выражения дают в результате полную неопределенность:
- бесконечность минус бесконечность;
- бесконечность умножить на 0;
- бесконечность разделить на бесконечность;
- ноль разделить на ноль;
- ноль умножить на бесконечность;
- ноль в нулевой степени;
- бесконечность в степени ноль;
- единица в степени бесконечность.
Задачи с неопределенностями возникают при вычислении пределов функций, которые заданы формулами, дающими подобные выражения при подстановке предельных значений аргумента. Математики говорят, что результатом таких уравнений будет бесконечное множество чисел. Обычно для их решения используют различные схемы и алгоритмы. Это называется раскрытием неопределенности.
Над нулем можно проделывать все арифметические операции. Единственное ограничение — он не может быть делителем для любого действительного числа. Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.
Источник
Уроки математики: умножение на ноль – главное правило
Впервые с таким арифметическим действием, как умножение, ученики знакомятся на школьной скамье. Учитель математики среди многочисленных правил поднимает тему «умножение на ноль». Несмотря на однозначность формулировки, у учащихся возникает множество вопросов. Давайте рассмотрим, что будет, если умножить на 0.
По две стороны спора
Правило, согласно которому умножать на ноль нельзя, порождает массу споров между преподавателями и их учащимися. Важно понимать, что умножение на ноль является спорным аспектом ввиду своей неоднозначности.
В первую очередь акцентируется внимание на отсутствии достаточного уровня знаний у учеников средней общеобразовательной школы. Переступая порог учебного заведения, участник образовательного процесса в большинстве случаев не задумывается о главной цели, которую необходимо преследовать.
Это интересно! Как раскрыть модуль действительного числа и что это такое
В течение обучения преподаватель освещает различные вопросы. В их число входит ситуация, что получится, если умножать на 0. Стремясь предвосхитить повествование преподавателя, некоторые ученики вступают в полемику. Они доказывают, по крайней мере, стараются, что умножение на 0 допустимо. Но, к сожалению, это не так. При умножении на 0 любого числа получается ровным счетом ничего. В некоторых литературных источниках даже встречается упоминание, что любое число, умноженное на ноль, образует пустоту.
Важно! Внимательные слушатели аудитории сразу схватывают, что если число умножить на 0, то в результате получится 0. Иное развитие событий прослеживается в случае тех учеников, кто систематически пропускает занятия. Невнимательные или недобросовестные учащиеся чаще остальных задумываются, сколько будет, если умножать на ноль.
В результате отсутствия знаний по теме преподаватель и нерадивый ученик оказываются по противоположные стороны противоречивой ситуации.
Различие во взглядах на тему спора заключается в степени образованности на предмет того, можно умножать на 0 или все-таки нет. Единственный допустимый выход из сложившейся ситуации — попытаться воззвать к логическому мышлению для поиска верного ответа.
Для объяснения правила не рекомендуется использовать следующий пример. У Вани в сумке лежат 2 яблока на перекус. В обед он задумался о том, чтобы положить в портфель еще сколько-нибудь яблок. Но в тот момент рядом не оказалось ни одного фрукта. Ваня не положил ничего. Иными словами, к 2 яблокам он поместил 0 яблок.
Это интересно! Считаем правильно: как находить процент от суммы и числа
В плане арифметики в данном примере получается, что если 2 умножить на 0, то не получается пустоты. Ответ в этом случае однозначный. Для этого примера правило умножения на ноль не актуально. Верное решение заключается в суммировании. Именно поэтому правильный ответ заключается в 2 яблоках.
В противном случае учителю не остается ничего иного, кроме как составить ряд заданий. Последняя мера — повторно задать прохождение темы и провести опрос на исключения в умножении.
Суть действия
Изучение алгоритма действий при умножении на ноль целесообразно начинать с обозначения сути арифметического действия.
Сущность действия умножить изначально определялась исключительно для натурального числа. Если раскрывать механизм действия, то определенное число, участвующее в вычислении, прибавляется к самому себе.
При этом важно учитывать количество прибавлений. В зависимости от данного критерия получается различный результат. Прибавление числа относительно самого себя определяет такое его свойство, ка натуральность.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Рассмотрим на примере. Необходимо число 15 умножить на 3. При умножении на 3 число 15 троекратно увеличивается в своей величине. Иными словами, действие выглядит как 15 * 3 = 15 + 15 + 15 = 45. Основываясь на механизме расчета, становится очевидным, если число умножить на другое натуральное число, возникает подобие сложения в упрощенном виде.
Алгоритм действий при умножении на 0 целесообразно начинать с предоставления характеристики на ноль.
Обратите внимание! Согласно общепринятому мнению ноль обозначает целое ничто. Для пустоты подобного рода в арифметике предусмотрено обозначение. Несмотря на данный факт, нулевое значение не несет под собой ничего.
Следует отметить, что подобное мнение в современном мировом научном обществе отличается от точки зрения древних восточных ученых. Согласно теории, которой они придерживались, ноль приравнивался к бесконечности.
Иными словами, если умножить на ноль, то получится многообразие вариантов. В нулевом значении ученые рассматривали некое подобие глубины мироздания.
В качестве подтверждения возможности умножить на 0 математики приводили следующий факт. Если рядом с любым натуральным числом поставить 0, то получится значение, превышающее исходное в десятки раз.
Приведенный пример является одним из аргументов. Кроме доказательства подобного рода, существует множество других примеров. Именно они лежат в основе непрекращающихся споров при умножении на пустоту.
Это интересно! Как найти и чему будет равна длина окружности
Целесообразность попыток
Среди учеников довольно часто на первых порах освоения учебного материала встречаются попытки число умножить на 0. Подобное действие является грубейшей ошибкой.
По существу от таких попыток ничего не произойдет, но и пользы не будет. Если произвести умножение на нулевое значение, то получится в дневнике неудовлетворительная отметка.
Единственная мысль, которая должна возникать при умножении на пустоту, — невозможность действия. Запоминание в данном случае играет немаловажную роль. Выучив правило раз и навсегда, учащийся предотвращает появление спорных ситуаций.
В качестве примера, применяемого при умножении на нулевое значение, разрешается использовать следующую ситуацию. Саша решила купить яблоки. Пока она была в супермаркете, она остановила выбор на 5 крупных спелых яблоках. Сходив в отдел молочной продукции, она посчитала, что этого ей будет недостаточно. Девочка положила к себе в корзину еще 5 штук.
Поразмыслив еще чуть-чуть, она взяла еще 5. В результате на кассе у Саши получилось: 5 * 3 = 5 + 5 + 5 = 15 яблок. Если бы она положила по 5 яблок только 2 раза, то было бы 5 * 2 = 5 + 5 = 10. В том случае, если бы Саша не положила в корзинку ни разу по 5 яблок, было бы 5 * 0 = 0 + 0 + 0 + 0 + 0 = 0. Иными словами, купить яблоки 0 раз значит не купить ни одного.
Полезное видео
Подведем итоги
Правило умножения на нулевое значение порождает множество споров. Для понимания его сути достаточно рассмотреть пару примеров. Только запоминание формулировки позволит уяснить, можно умножать на 0 или нет.
Источник
Действия с нулём
В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат.
Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно — тоже) было разделено на «ничто».
Примеры вычисления
С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение. Приведем примеры их осуществления и некоторые пояснения к ним.
Сложение
При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.
Пример 1
Двадцать четыре плюс ноль равняется двадцать четыре.
24 + 0 = 24
Пример 2
Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.
Вычитание
При вычитании нуля из некоторого числа (целого, дробного, положительного или отрицательного) оставляет его полностью неизменным.
Пример 1
Две тысячи сто пятьдесят два минус ноль равняется две тысячи сто пятьдесят два.
2152 — 0 = 2152
Пример 2
Сорок одна целая три пятых минус ноль равняется сорок одна целая три пятых.
Умножение
При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль.
Пример 1
Пятьсот восемьдесят шесть умножить на ноль равняется ноль.
586 × 0 = 0
Пример 2
Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль.
0 × 135 = 0
Пример 3
Ноль умножить на ноль равняется ноль.
0 × 0 = 0
Деление
Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?
В тех случаях, когда ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.
Пример 1
Ноль разделить на двести шестьдесят пять равняется ноль.
0 : 265 = 0
Пример 2
Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль.
Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.
0 : 0 = 8 ибо 8 × 0 = 0
В математике такая задача, как деление нуля на ноль, не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.
Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в ноль. Если это определено, то такому выражению, как ноль разделить на ноль, в подавляющем большинстве случаев можно придать некий смысл.
Источник
При умножении числа на нуль получаем нуль.
Арифметические операции над положительными рациональными числами
· Сложение
· Вычитание
· Умножение
· Деление
Сложение.
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.
Пример 1. Найти сумму 2,5 + 3,2.
Решение. Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:
2,5 + 3,2 = 5,7
следует, что в результате сложения двух положительных чисел получится положительное число.
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a
Вычитание.
Вычитание — действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b= a следует, что a−b=c a−c=b.
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому.
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Произведение любого рационального числа a на нуль есть нуль.
множение любого рационального числа a на 1 дает число a.
Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а*а^-1=1
При умножении любого числа на -1 получится число противоположное данному: 2,5 · (-1) = -2,5
Деление
Деление — действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b·c =a, следует, что a:b =c и a:c=b
При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс
При делении любого числа на -1 получится число противоположное данному: 2,5 : (-1) = -2,5
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Разделить число а на число b, отличное от нуля — то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a⋅b^−1 . Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Cвойства арифметических операций
Свойства сложения
1. Переместительный (коммуникативный) закон сложения: a + b = b + a.
От перемены мест слагаемых сумма не меняется.
Примеры:
45 + 21 = 21 + 45 = 66;
104 + 0 = 0 + 104 = 104.
2. Сочетательный (ассоциативный) закон сложения: a + b + c = a + (b + c).
Сумма не меняется, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой. Пример:
197 + 23 + 77 = 197 + (23 + 77) = 197 + 100 = 297.
Примечание: оба закона справедливы для любого количества слагаемых.
3. a + 0 = 0 + a = 0.
Прибавление к числу нуля не изменяет этого числа.
Пример:
99 + 0 = 0 + 99 = 99.
Свойства вычитания
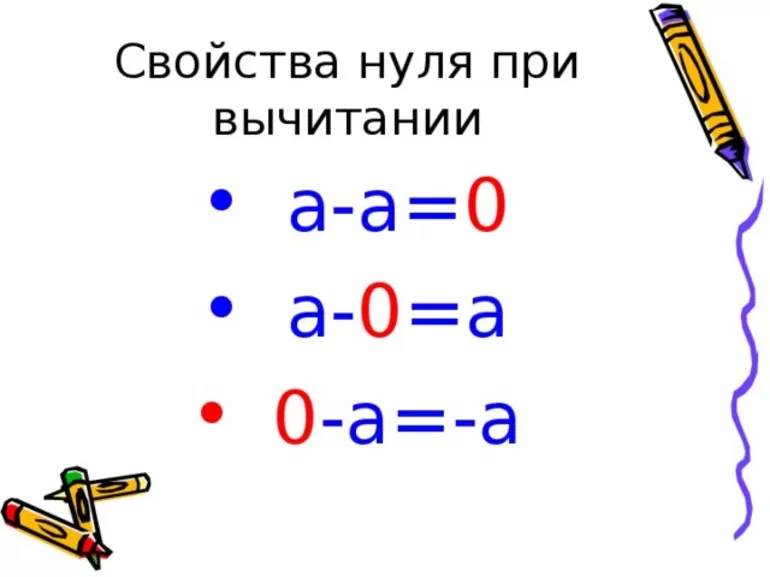
1. a — 0 = a.
Вычитание нуля из числа не изменяет этого числа
Пример:
17 — 0 = 17.
2. a — a = 0.
Если из числа вычесть само это число, то разность равна нулю.
Пример:
276 — 276 = 0
Вычитание суммы из числа: a — (b + c) = a — b — c.
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
Пример:
183 — (43 + 19) = 183 — 43 — 19 = 140 — 19 = 121.
4. Вычитание числа из суммы: (a + b) — c = (a — c) + b = a + (b — c).
Чтобы вычесть число из суммы, можно вычесть это число из какого-нибудь одного слагаемого и полученную разность прибавить к сумме остальных слагаемых.
Примеры:
(143 + 27) — 33 = (143 — 33) + 27 = 110 +27 = 137;
(277 + 31 + 759) — 559 = (277 + 31) + (759 — 559) = 308 + 200 = 508.
5. Прибавление разности к числу: а + (b — c) = a + b — c.
Чтобы прибавить разность к числу, можно прибавить к нему уменьшаемое и из полученной суммы вычесть вычитаемое.
Пример:
543 + (202 — 45) = 543 + 202 — 45 = 745 — 45 = 700.
Свойства умножения
1. Переместительный (коммуникативный) закон умножения: а · b = b · а.
От перемены мест множителей произведение не меняется.
Пример:
569 · 17 = 17 · 569.
2. Сочетательный (ассоциативный) закон умножения: а · b · c = а · (b · c).
Произведение не изменится, если какую-нибудь группу рядом стоящих множителей заменить их произведением.
Пример:
39 · 25 · 4 = 39 · (25 · 4) = 39 · 100 = 3900.
3. Распределительный (дистрибутивный) закон умножения относительно сложения: (а + b + c) · d = аd + bd + cd.
Произведение суммы нескольких чисел на какое-нибудь число равно сумме произведений каждого слагаемого на это число.
Пример:
(150 + 75 + 12) · 4 = 150 · 4 + 75 · 4 + 12 · 4 = 600 + 300 + 48 = 948
4. Распределительный (дистрибутивный) закон умножения относительно вычитания: (а — b) · c = аc — bc.
Чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе.
Пример:
(125 — 42) · 8 = 125 · 8 — 42 · 8 = 1000 — 336 = 664.
5. а · 1 = 1 · а = а.
При умножении числа на единицу получаем само число.
Пример:
45 · 1 = 1 · 45 = 45.
6. а · 0 = 0 · а = 0.
При умножении числа на нуль получаем нуль.
Пример:
6999 · 0 = 0 · 6999 = 0.
Примечание. Если в произведении нескольких множителей хотя бы один из множителей равен нулю, то произведение равно нулю.
Свойства деления
1. a : 1 = a.
При делении числа на единицу получаем само число.
Пример:
503 : 1 = 503.
2. 0 : a = 0.
При делении нуля на любое число, не равное нулю, получаем нуль.
Пример:
0 : 941 = 0.
3. На нуль делить нельзя!
4. a : a = 1.
При делении числа, не равного нулю, на само себя, получаем единицу.
Пример:
67 : 67 = 1.
5. Деление суммы на число: (a + b) : c = a : c + b : c.
Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
Пример:
(545 + 75) : 5 = 545 : 5 + 75 : 5 = 109 + 15 = 124.
6. Деление разности на число: (a — b) : c = a : c — b : c.
Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.
Пример:
(633 — 99) : 3 = 633 : 3 + 99 : 3 = 211 + 33 = 244.
7. Деление произведения на число: (a · b) : c = (a : c) · b = a · (b : c).
Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.
Пример:
(77 · 9) : 7 = (77 : 7) · 9 = 11 · 9 = 99.
©2015-2021 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-08-04 Нарушение авторских прав и Нарушение персональных данных
Источник